Nice to meet you
Hello, I'm Alex
Software Developer & Problem Solver
Welcome to my portfolio! With expertise in Python, Django, JavaScript, and a bit of cloud technologies, I build solutions that make an impact. As a glimpse into my journey and skills, please explore this featured projects:
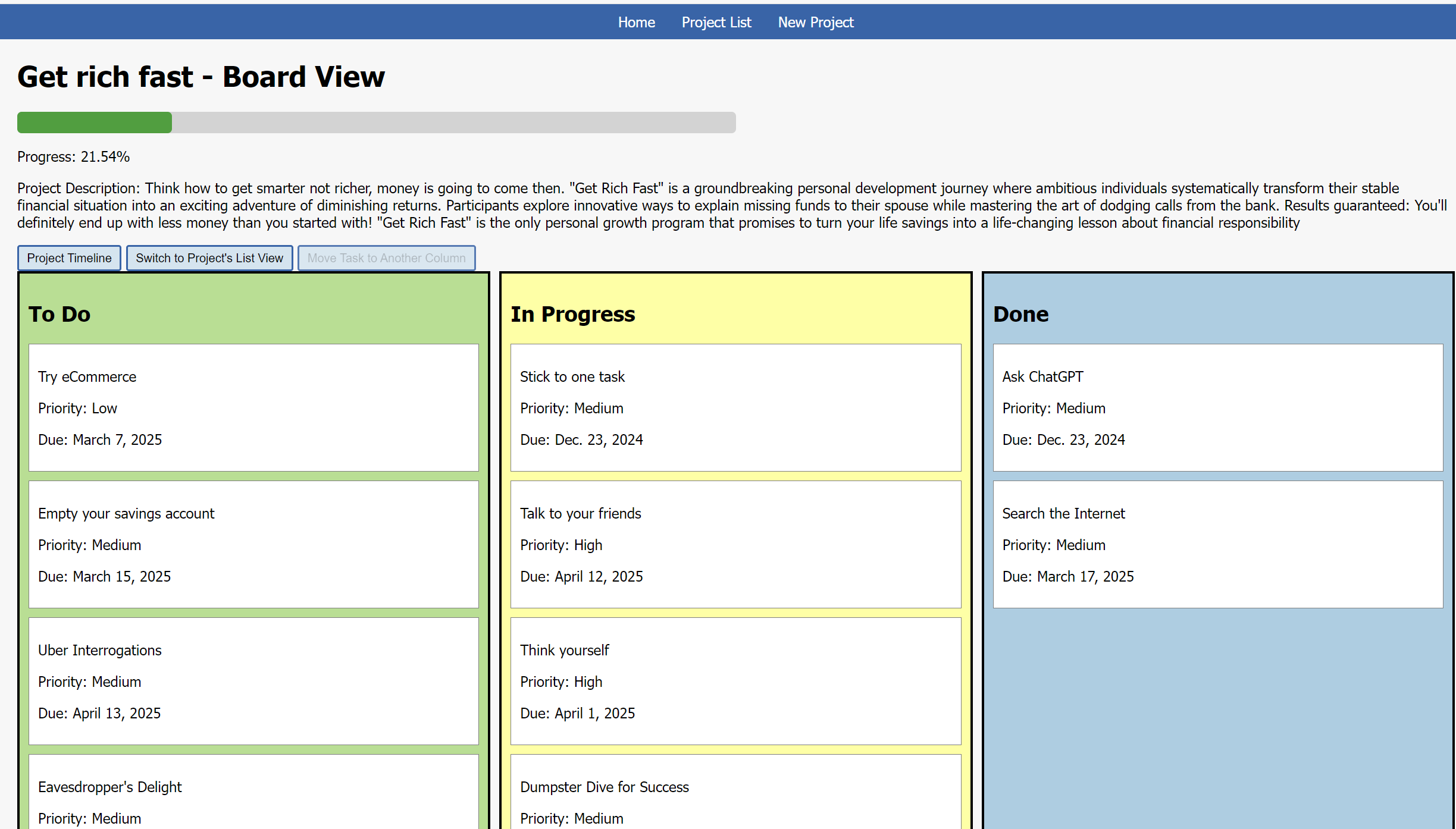
Project Management System
A simple yet powerful app to manage and visualise tasks with intuitive views. Built with Django to ensure robustness and future scalability.
A new version of PMS MVP incorporates a robust API for enhanced flexibility and integration, now deployed within a Docker container on an AWS EC2 instance.